In this problem, you are to use the result of Problem 129 to derive Equation 14-45, which relates the width of the resonance curve to the Q value when the resonance is sharp. At resonance, the denominator of the fraction in brackets in Equation 14-51 is b²ώ₀² and P_av has its maximum value. For a sharp resonance, the variation in w in the numerator in Equation 14-51 can be neglected. Then the power input will be half its maximum value at the values of w, for which the denominator is 2b² ώ₀².

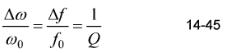
(a) Show that w then satisfies.

(b) Using the approximation ώ + ώ₀ ≈ 2ώ₀, show that

(c) Express b in terms of Q.

(d) Combine the results of (b) and (c) to show that there are two values of w for which the power input is half that at resonance and that they are given by

Therefore, ώ₂ – ώ₁ = ∆ώ = ώ₀/Q, which is equivalent to Equation 14-45.

f 14-45 fo ) -1