Let the r.v.sXandYhave the Bivariate normal distribution with parameters μ₁, μ₂in Â, 0 < s₁, s₂< ¥, andrÃŽ [€“ 1, 1] so that their joint probability density function (p.d.f.) is given by

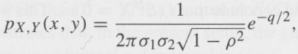
Where

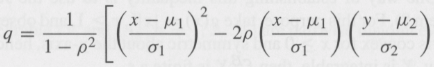
(i) Show that the exponent may be written thus:

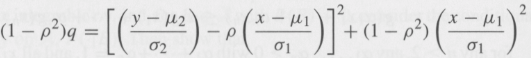
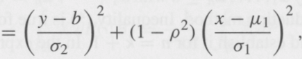
Where b = m₂ + rs₂/s¹ (x €“ m₁)

(ii) From part (i), it follows that:

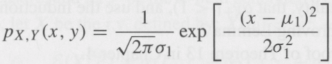
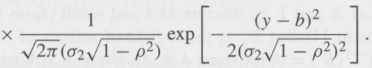
From this expression, and without any actual integration, conclude that the r.v. X is distributed as N (m₁, s²₁); i.e., X ~ N (μ₁, s²₁), and by symmetry, Y ~ N (m₂, s²₂).

Px,y(x, y) = 221- ? e 9/2