![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


-1.png)
-2.png)
-3.png)
-1.png)
-2.png)
-3.png)
-1.png)
-2.png)
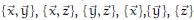
-1.png)
-2.png)
-3.png)

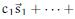
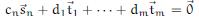
-1.png)
-2.png)
-3.png)
-1.png)
-2.png)
-3.png)
-1.png)
-2.png)
-3.png)
-1.png)
-2.png)
.png)
.png)
.png)
![ER' |x-w+z= 0]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/image/images12/961-M-L-A-L-S(5246).png)
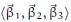
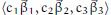
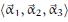
-1.png)
-2.png)

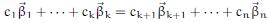
-1.png)
-2.png)
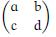
.png)
.png)
-1.png)
-2.png)
-1.png)
-2.png)
-1.png)
-2.png)
-3.png)
.png)
-1.png)
-2.png)
-3.png)
.png)
-1.png)
-2.png)
.png)
.png)
.png)
.png)
-1.png)
-2.png)
-3.png)
.png)
-1.png)
-2.png)