What is the interaction between the property of linear independence and the operation of union?

(a) We might conjecture that the union S∪T of linearly independent sets is linearly independent if and only if their spans have a trivial intersection  What is wrong with this argument for the ‘if’ direction of that conjecture? “If the union S ∪ T is linearly independent then the only solution to 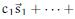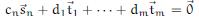is the trivial one c₁ = 0, . . . , d_m = 0. So any member of the intersection of the spans must be the zero vector because in  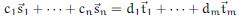each scalar is zero.”

(b) Give an example showing that the conjecture is false.

(c) Find linearly independent sets S and T so that the union of S - (S ∩ T) and T -(S∩T) is linearly independent, but the union S∪T is not linearly independent.

(d) Characterize when the union of two linearly independent sets is linearly independent, in terms of the intersection of spans.

S]n (T) = (0)-