A storage tank contains a liquid at depth y where y = 0 when the tank is half full. Liquid is withdrawn at a constant flow rate Q to meet demands. The contents are resupplied at a sinusoidal rate 3Q sin² (t).

Equation (1.13) can be written for this system as

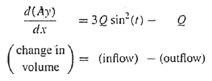
Or, since the surface area A is constant

dy/dx = 3 Q/A sin² (t) – Q/A

Use Euler’s method to solve for the depth y from t = 0 to 10 d with a step size of 0.5 d. The parameter values are A = 1200 m² and Q = 500 m³/d. Assume that the initial condition is y = 0.

d(Ay) = 3Q sin () - e dx change in (inflow) - (outflow) volume=