A student has Laplace transformed an ordinary differential equation (ODE) and obtained the following transform:

.

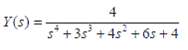The following facts are known:

(i) The original ODE had all zero initial conditions.

(ii) Its only Input was sin wt where the radian frequency w =?2.

(a) What can you say about the original ODE? In other words, determine what it was to the maximum extent possible.

(b) Is your result unique? Or are there other possible forms of the ODE that lead to the same Y(s)?

(c) Without finding y(t), what functions of time will be in the solution?

Y(s) =+3s + 45 + 6s + 4