The first-order differential equation dy/dx = x² + y² cannot be solved in terms of elementary functions. However, a solution can be expressed in terms of Bessel functions.

(a) Show that the substitution y = -1/u du/dx leads to the equation u'' + x²u = 0.

(b) Use (18) in Section 6.4 to find the general solution of u'' + x²u = 0.

(c) Use (20) and (21) in Section 6.4 in the forms

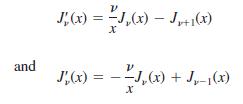
as an aid to show that a one-parameter family of solutions of dy/dx = x² + y² is given by

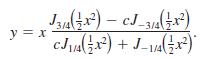
J,(x) = J,(x) Jrt1(x) and J',(x) = --J,(x) + J,-(x)