By the principles used in modeling the string it can be shown that small free vertical vibrations of a uniform elastic beam (Fig. 292) are modeled by the fourth-order PDE

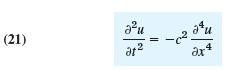
where c² = EI/ρA (E = Young€™s modulus of elasticity, I = moment of intertia of the cross section with respect to the y-axis in the figure, ρ = density, A = cross-sectional area).

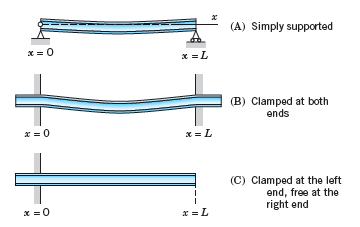
If the beam is clamped at the left and free at the right (Fig. 293C), the boundary conditions are

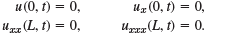
Show that F in Prob. 15 satisfies these conditions if βL is a solution of the equation

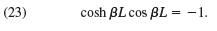
Find approximate solutions of (23).

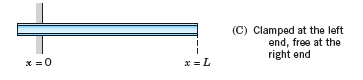
Data from Prob. 15

By the principles used in modeling the string it can be shown that small free vertical vibrations of a uniform elastic beam (Fig. 292) are modeled by the fourth-order PDE

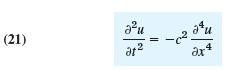
where c² = EI/ρA (E = Young€™s modulus of elasticity, I = moment of intertia of the cross section with respect to the y-axis in the figure, ρ = density, A = cross-sectional area).

Substituting u = F(x)G(t) into (21), show that

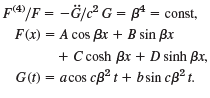
, at2 a .4 |(21) u(0, t) = 0, Uz (0, t) = 0, Urzz(L, t) = 0. Uxz (L, t) = 0,