By the principles used in modeling the string it can be shown that small free vertical vibrations of a uniform elastic beam (Fig. 292) are modeled by the fourth-order PDE

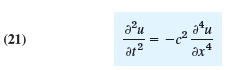where c² = EI/ρA (E = Young’s modulus of elasticity, I = moment of intertia of the cross section with respect to the y-axis in the figure, ρ = density, A = cross-sectional area).

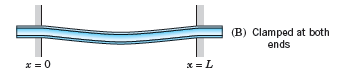
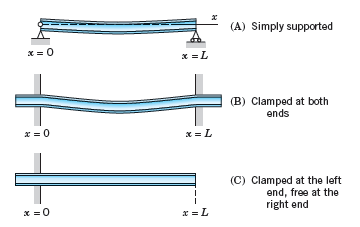
What are the boundary conditions for the clamped beam in Fig. 293B? Show that F in Prob. 15 satisfies these conditions if βL is a solution of the equation

Determine approximate solutions of (22), for instance, graphically from the intersections of the curves of cos βL and 1/cosh βL. 

Data from Prob. 15

By the principles used in modeling the string it can be shown that small free vertical vibrations of a uniform elastic beam (Fig. 292) are modeled by the fourth-order PDE

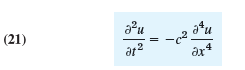where c² = EI/ρA (E = Young’s modulus of elasticity, I = moment of intertia of the cross section with respect to the y-axis in the figure, ρ = density, A = cross-sectional area).

Substituting u = F(x)G(t) into (21), show that

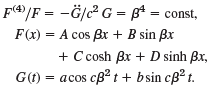
(21) a2u at = ar'