Consider (n) real equal-mass scalar fields (phi_{1}, ldots, phi_{n}) with a quartic interaction of the form (mathcal{L}_{text {int }}=-(lambda / 4 !)left(phi_{1}^{2}+cdots+phi_{n}^{2} ight)^{2}), then (a)

Consider \(n\) real equal-mass scalar fields \(\phi_{1}, \ldots, \phi_{n}\) with a quartic interaction of the form \(\mathcal{L}_{\text {int }}=-(\lambda / 4 !)\left(\phi_{1}^{2}+\cdots+\phi_{n}^{2}\right)^{2}\), then

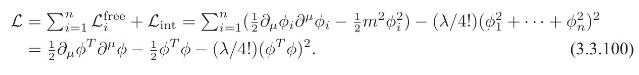
(a) Obtain the Euler-Lagrange equations for this theory.

(b) Explain why this theory is invariant under \(O(n)\) transformations. Derive the conserved Noether current and explain why it corresponds to the \(S O(n)\) subgroup and not \(O(n)\).

(c) For \(n\) complex equal-mass scalar fields write a corresponding Lagrangian density invariant under \(U(n)\). Obtain the Euler-Lagrange equations. Construct the conserved Noether current.

L= C= Lfree = =1+ Lint = -1(0000; - m) - (A/4!) (o + + ) - - (X/4!)(6). (3.3.100)