A Lagrangian density with two complex scalar fields, \(\phi\) and \(\chi\), is given by

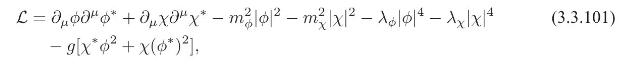
where \(m_{\phi}, m_{\chi}, \lambda_{\phi}, \lambda_{\chi}, g\) are real constants.

(a) Using the transformations \(\phi \rightarrow e^{i \alpha} \phi\) and \(\chi \rightarrow e^{i \beta} \chi\) choose \(\alpha, \beta\) such that \(\mathcal{L}\) is invariant. Construct the Noether current \(j^{\mu}\).

(b) Use the Euler-Lagrange equations to verify that \(\partial_{\mu} j^{\mu}(x)=0\).

L = * + X x* - m | o| m |x|-4-Xxx - (3.3.101) - 9[x* + x(0*)],