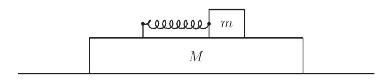
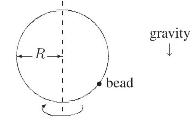
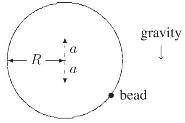
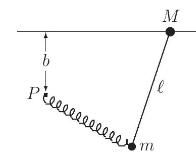
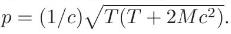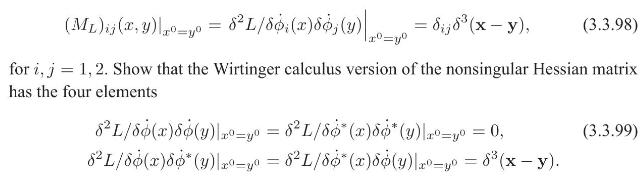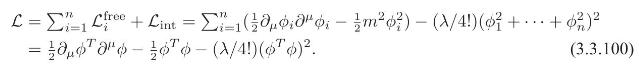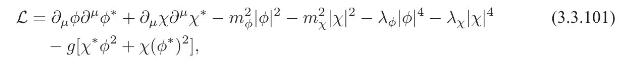Introduction To Quantum Field Theory Classical Mechanics To Gauge Field Theories 1st Edition Anthony G. Williams - Solutions

Discover comprehensive support for "Introduction To Quantum Field Theory: Classical Mechanics To Gauge Field Theories 1st Edition" by Anthony G. Williams. Access our online repository featuring an extensive answers key and solutions manual, perfect for enhancing your understanding. Our solutions PDF includes detailed, step-by-step answers to solved problems, providing clarity on textbook questions and answers. Benefit from chapter solutions and test bank resources tailored for students and instructors alike. With free download options, our instructor manual equips you with the tools needed for mastery. Dive into the world of quantum field theory with confidence.