We define a free complex scalar field as (phi(x)=(1 / sqrt{2})left[phi_{1}(x)+i phi_{2}(x) ight] in mathbb{C}) in terms
Question:
We define a free complex scalar field as \(\phi(x)=(1 / \sqrt{2})\left[\phi_{1}(x)+i \phi_{2}(x)\right] \in \mathbb{C}\) in terms of two real free scalar fields \(\phi_{1}(x), \phi_{2}(x) \in \mathbb{R}\) and the Lagrangian density as the sum of the two free Lagrangian densities.
(a) Show that the Lagrangian density in terms of \(\phi(x)\) and \(\phi^{*}(x)\) is as given in Eq. (3.2.48), \(\mathcal{L}=\left(\partial_{\mu} \phi\right)^{*}\left(\partial^{\mu} \phi\right)-m^{2} \phi^{*} \phi\). Using the Euler-Lagrange equations for \(\phi_{1}\) and \(\phi_{2}\) show that the complex scalar field and its complex conjugate satisfy \(\left(\partial_{\mu} \partial^{\mu}+m^{2}\right) \phi(x)=\left(\partial_{\mu} \partial^{\mu}+\right.\) \(\left.m^{2}\right) \phi^{*}(x)=0\).
(b) Using the action \(S[\phi]=\int d^{4} x \mathcal{L}\) and the Wirtinger calculus in Sec. A.2.5, show that these equations of motion follow from Hamilton's principle, \(\delta S[\phi] / \delta \phi^{*}(x)=\delta S[\phi] / \delta \phi(x)=0\).
(c) Using Eq. (3.1.15) evaluate the conjugate momenta \(\pi(x)\) and \(\pi^{*}(x)\). Use these results to construct the Hamiltonian using Eq. (3.1.16) and show that \(H=\int d^{3} x \mathcal{H}=\) \(\int d^{3} x\left[\pi^{*}(x) \pi(x)+\boldsymbol{abla} \phi^{*}(x) \cdot \boldsymbol{abla} \phi(x)+m^{2} \phi^{*}(x) \phi(x)\right]\).
(d) Obtain Hamilton's equations using Eq. (3.1.21) in terms of \(\phi\) and \(\phi^{*}\) and show that these reproduce the Klein-Gordon equations for \(\phi\) and \(\phi^{*}\).
(e) The complex scalar field Lagrangian in terms of \(\phi_{1}\) and \(\phi_{2}\) has a well-defined Legendre transform since the Hessian matrix \(M_{L}\) is positive definite. This follows from the straightforward generalization of Eq. (3.1.48),
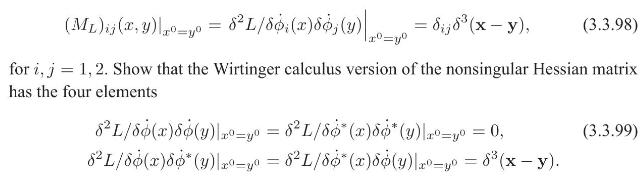
Step by Step Answer:

Introduction To Quantum Field Theory Classical Mechanics To Gauge Field Theories
ISBN: 9781108470902
1st Edition
Authors: Anthony G. Williams





