Develop an M-file function based on Fig. 9.5 to implement Gauss elimination with partial pivoting. Modify the function so that it computes and returns the determinant (with the correct sign), and detects whether the system is singular based on a near-zero determinant. For the latter, define “near-zero” as being when the absolute value of the determinant is below a tolerance. When this occurs, design the function so that an error message is displayed and the function terminates. Here is the functions first line:

function [x, D] = GaussPivotNew(A, b, tol)
where D = the determinant and tol = the tolerance. Test your program for Prob. 9.5 with tol = 1 × 10⁻⁵.

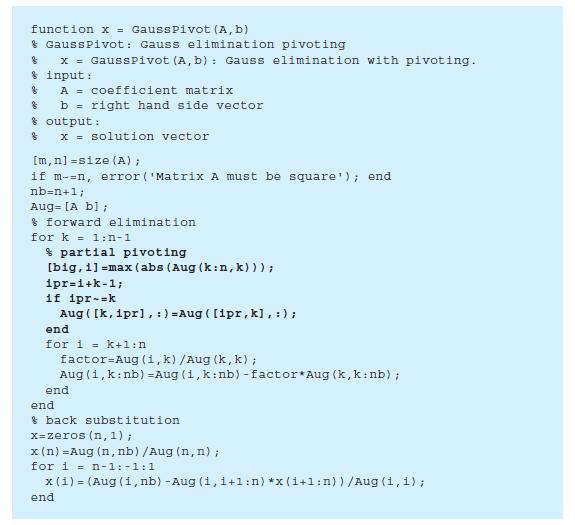
function x = Gauss Pivot (A, b) & Gauss Pivot: Gauss elimination pivoting 8 x = GaussPivot (A,b): Gauss elimination with pivoting. & input: & A = coefficient matrix f b = right hand side vector & output: $ x = solution vector [m, n] =size (A); if m-=n, error('Matrix A must be square'); end nb=n+1; Aug= [A b]; & forward elimination for k=1:-1 & partial pivoting [big, 1] =max (abs (Aug (k:n, k))); 1pr=1+k-1; if ipr-=k Aug ( [k, ipr], :) = Aug ( [ipr, k], :); end for i=k+1:n factor=Aug (1,k)/Aug (k, k); Aug (1,k: nb) =Aug (i, k: nb) -factor Aug (k, k: nb); end end & back substitution x=zeros (n, 1); x (n) =Aug (n, nb) /Aug (n, n) ; for in-1:-1:1 x(i)= (Aug (i, nb) -Aug (i,i+1:n) *x (i+1:n))/Aug (1, 1); end