Make the given changes in the indicated examples of this section and then solve the resulting problems.

In Example 3, change the − sign before 8x to + and then sketch the graph.

Data from Example 3

For the graph of the function y = 2x² − 8x + 6, find the vertex and y-intercept and sketch the graph. (This function was also used in Example 2.) First, a = 2 and b = −8. This means that the x-coordinate of the vertex is

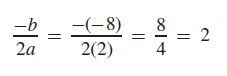
and the y-coordinate is y = 2(2²) − 8(2) + 6 = −2
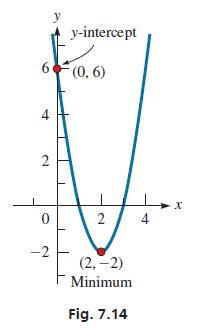
Thus, the vertex is (2, −2). Because a > 0, it is a minimum point. Because c = 6, the y-intercept is (0, 6).

We can use the minimum point (2, −2) and the y-intercept (0, 6), along with the fact that the graph is a parabola, to get an approximate sketch of the graph. Noting that a parabola increases (or decreases) away from the vertex in the same way on each side of it (it is symmetric with respect to a vertical line through the vertex), we sketch the graph in Fig. 7.14. It is the same graph as that shown in Fig. 7.13(a).

Transcribed Image Text:

b 2a || -(-8) 2(2) || ∞14 || 2