Make the given changes in the indicated examples of this section and then solve the resulting quadratic equations by completing the square.

In Example 2, change the − sign before 6x to +.

Data from Example 2

To find the roots of the quadratic equation
x² − 6x − 8 = 0
first note that the left side is not factorable. [However, x² − 6x is part of the special product (x − 3)² = x² − 6x + 9 and this special product is a perfect square.] By adding 9 to x² − 6x, we have (x − 3)² . Therefore, we rewrite the original equation as

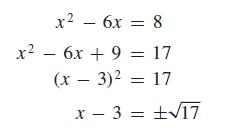
The ± sign means that x − 3 = √17 or x − 3 = − √17.

By adding 3 to each side, we obtain x = 3 ± √17

which means x = 3 + √17 and x = 3 − √17 are the two roots of the equation. Therefore, by adding 9 to x² − 6x on the left, we have x² − 6x + 9, which is the perfect square of x − 3. This means, by adding 9 to each side, we have completed the square of x − 3 on the left side. Then, by equating x − 3 to the positive and negative square root of the number on the right side, we were able to find the two roots of the quadratic equation by solving two linear equations.

x - 6x = 8 x - 6x + 9 = 17 (x 3)2 = 17 - x - 3 = 17