Make the given changes in the indicated examples of this section and then solve the resulting problems.

In Example 7, change 38 to 42 and then answer the questions.

Data from Example 7

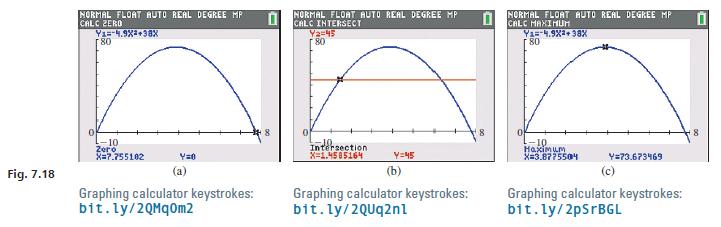
A projectile is fired vertically upward from the ground with a velocity of 38 m/s. Its distance above the ground is given by s = -4.9t + 38t, where s is the distance (in m) and t is the time (in s). Graph the function, and from the graph determine (1) when the projectile will hit the ground, (2) how long it takes to reach 45 m above the ground, and (3) the maximum height of the projectile. 1. To find when the projectile hits the ground, we set the height s = 0 and then solve for t. This results in the equation -4.9t + 38t = 0. Graphically, this is the x-intercept of the function y = -4.9t2 + 38t, which can be found using the zero feature on a calculator. The solution is t = 7.76 s as shown in Fig. 7.18(a). 2. To find when the projectile is 45 m above the ground, we can use the intersect feature to find the points of intersection between the given function and the hori- zontal line y = 45. There are two solutions: t = 1.46 s and t = 6.30 s. The first of these solutions is shown in Fig. 7.18(b). 3. The maximum height occurs at the vertex, which can be found using the maxi- mum feature on a calculator. From Fig. 7.18(c), we see that the maximum height is 73.7 m, which occurs after 3.88 s.