A point mass (m) is located at the origin. Let (Q) be the flux of the gravitational

Question:

A point mass $m$ is located at the origin. Let $Q$ be the flux of the gravitational field $\mathbf{F}=-G m \frac{\mathbf{e}_{r}}{r^{2}}$ through the cylinder $x^{2}+y^{2}=R^{2}$ for $a \leq z \leq b$, including the top and bottom (Figure 18). Show that $Q=-4 \pi G m$ if \(a

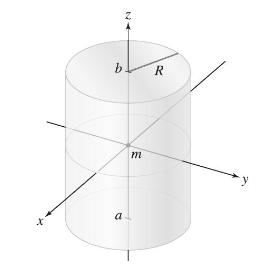
b a m R