Question: Let v(t) = r '(t). Show that N(t) v(t)r'' (t) - v'(t)r' (t) |v(t)r(t) - v'(t)r' (t)||

Let v(t) = ΙΙr '(t)ΙΙ. Show that

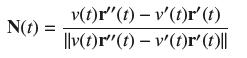
N(t) v(t)r''(1) - v' (t)r' (t) |v(t)r

N is the unit vector in the direction T'(t). Differentiate T(t) = r'(t)/v(t) to show that v(t)r"(t) − v'(t)r (t) is a positive multiple of T '(t).

N(t) v(t)r'' (t) - v'(t)r' (t) |v(t)r"(t) - v'(t)r' (t)||

Step by Step Solution

★★★★★

3.32 Rating (146 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

Since vt r t and Tt is a unit vector in the direction at r t we may write r t ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Q:

Suppose variables x,y denote people. Y(x,y) denotes "x is younger than y". F (x,y) denotes "x is a friend of y". Translate the following sentences into logic: a. Emma is the youngest person b. Ruth...

Q:

Lawson Consulting had the following accounts and amounts on December 31. The Retained Earnings account balance at December 1 was $0 and the owner invested $16,070 cash in the company on December 1....

Q:

In matlab please. Array access and modification Perform all the following operations in a script using array operations! Make sure you document it properly and minimize the # of operations. Each of...

Q:

Let G = (V, E) be a connected, undirected graph. (In this course we follow the usual convention that, unless indicated otherwise, an undirected graph does not have loops or multiple edges.) As usual...

Q:

Let V C R" be a subspace. Define VI = (u e R" : u is orthogonal to V). In other words, V = (u ER" : u . v = 0 for all v E V). (a) (2 points) Show that Vis a subspace of R". (Hint: use Remark...

Q:

Problem 4 Let V = {z R, x > 0} be the set of positive real numbers and let us define the following operations on V: +v: VXV = V (fa = xy and v RxV V \\z) - 2 we use when we see x in the abstract...

Q:

4. Let V C R" be a subspace. Define VI = {u e R" : u is orthogonal to V). In other words V! = {u e R" : for all v E V, u . v = 0). (a) (2 points) Show that V- is a subspace of R".(b) (3 points) Let v...

Q:

I don't understand the initial proof Problem 8.12 (the Projection Matrix). If a is a scalar, the function f : R" -> R" defined as y = f(x) = ax, with x E R", gives a vector y E R" that is always...

Q:

Linear algebra Question 1 (a) Find the rank of the following matrix for all values of a 3 1 1 4 a 4 10 1 1 7 17 3 2 2 4 3 Show your working. [4 Marks] (b) Let A and B be matrices of size 2 x 3 and 3...

Q:

You can only answer 3 of questions if you can make them correct Question 1 (a) Find the rank of the following matrix for all values of a 3 1 1 4 a 4 10 1 1 7 17 3 2 2 4 3 Show your working. [4 Marks]...

Q:

Determine whether the company should purchase the new machine. (Enter negative amounts using either a negative sign preceding the number e.g. -45 or parentheses e.g. (45). Do not leave any field...

Q:

Discuss the high-level conceptual architecture for major elements and relationships in Big Data Solutions. 2. What are the similarities and differences between high-level conceptual architecture and...

Q:

Yes, it's highly likely that JAL's forward contracts constituted an economic hedge, meaning losses on the contracts were offset by gains on its operations, as JAL used them to mitigate the impact of...

Q:

The pervasive presence of EEO laws and regulations has resulted in the HR staff assuming much of the responsibility to ensure that an organizations employment policies and practices comply with these...

Q:

A store sells cashews for $5.00 per pound and peanuts for $1.50 per pound. The manager decides to mix 30 pounds of peanuts with some cashews and sell the mixture for $3.00 per pound. How many pounds...

Q:

A recently retired couple needs $12,000 per year to supplement their Social Security. They have $150,000 to invest to obtain this income. They have decided on two investment options:AA bonds yielding...

Q:

With a tail wind, a small Piper aircraft can fly 600 miles in 3 hours. Against this same wind, the Piper can fly the same distance in 4 hours. Find the average wind speed and the average airspeed of...

Q:

which IP addresses are valid

Q:

Whitewater Instruments sold $400 million of 10% bonds, dated January 1, on January 1, 2016. The bonds mature on December 31, 2035 (20 years). For bonds of similar risk and maturity, the market yield...

Q:

Which of the following actions did you take the #NAME? Error value in cell C 9 on the result worksheet?