Question: Consider two inductors L 1 and L 2 connected in parallel as shown in Figure P21.45. These two inductors act as one equivalent inductance L
Consider two inductors L1 and L2 connected in parallel as shown in Figure P21.45. These two inductors act as one equivalent inductance Lequiv. To find Lequiv, we first notice that because they are connected in parallel, the voltage across L1 and L2 must be the same, but the rate at which the current changes with time ΔI/Δt is different for the two inductors. Use these facts to write the total voltage across the two inductors in the form of Equation 21.23, where L is now the equivalent inductance, and find Lequiv. Note: The general result for many inductors in parallel is 1/ equiv Lequiv = 1/L1 + 1/L2 + 1/L3 +…...
Figure P21.45.
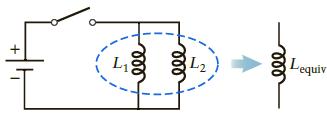
L1 Lequiv Figure P21.45 all
Step by Step Solution
3.45 Rating (171 Votes )
There are 3 Steps involved in it
To find the total potential drop across both inductors we use the general equation for th... View full answer

Get step-by-step solutions from verified subject matter experts


