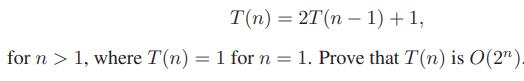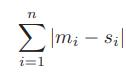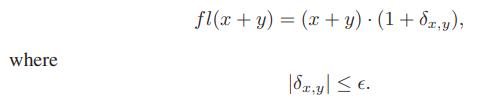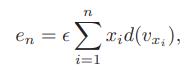![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


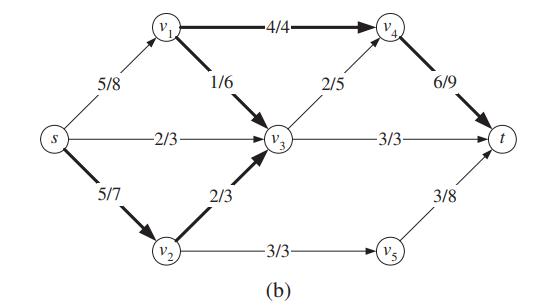
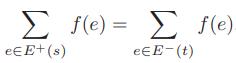
![Algorithm AllPairsShortestPaths(G): Input: A simple weighted directed graph G without negative-weight cycles Output: A numbering v1, v2, ..., Un of the vertices of G and a matrix D, such that D[i, j] is the distance from vị to v; in G let v1, v2, ..., Vn be an arbitrary numbering](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1595/3/1/4/3715f1690c3bc1531595314367241.jpg)
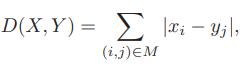
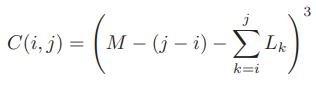
![Algorithm StoogeSort(A, i, j): Input: An array, A, and two indices, i and j, such that 1 < i 2 then m - [n/3] StoogeSort(A, i, j – m) StoogeSort(A, i+m, j) StoogeSort(A, i, j – m) // Sort the first part // Sort the last part // Sort](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1594/7/9/9/1705f0eb442013911594799163510.jpg)
![Algorithm StoogeSort(A, i, j): Input: An array, A, and two indices, i and j, such that 1 < i 2 then m - [n/3] StoogeSort(A, i, j – m) StoogeSort(A, i+m, j) StoogeSort(A, i, j – m) // Sort the first part // Sort the last part // Sort](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1594/7/9/8/9325f0eb354c984f1594798925460.jpg)