Question: For block diagram shown below, (mathrm{C}(s) / mathrm{R}(s)) is given by (a) (frac{mathrm{G}_{1} mathrm{G}_{2} mathrm{G}_{3}}{1+mathrm{H}_{2} mathrm{G}_{2} mathrm{G}_{3}+mathrm{H}_{1} mathrm{G}_{1} mathrm{G}_{2}}) (b) (frac{mathrm{G}_{1} mathrm{G}_{2} mathrm{G}_{3}}{1+mathrm{G}_{1} mathrm{G}_{2} mathrm{G}_{3}

For block diagram shown below, $\mathrm{C}(s) / \mathrm{R}(s)$ is given by

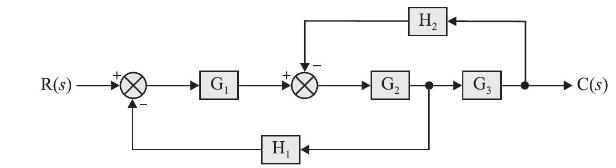
R(S) G G H G C(s)

(a) $\frac{\mathrm{G}_{1} \mathrm{G}_{2} \mathrm{G}_{3}}{1+\mathrm{H}_{2} \mathrm{G}_{2} \mathrm{G}_{3}+\mathrm{H}_{1} \mathrm{G}_{1} \mathrm{G}_{2}}$
(b) $\frac{\mathrm{G}_{1} \mathrm{G}_{2} \mathrm{G}_{3}}{1+\mathrm{G}_{1} \mathrm{G}_{2} \mathrm{G}_{3} \mathrm{H}_{1} \mathrm{H}_{2}}$
(c) $\frac{\mathrm{G}_{1} \mathrm{G}_{2} \mathrm{G}_{3}}{1+\mathrm{G}_{1} \mathrm{G}_{2} \mathrm{G}_{3} \mathrm{H}_{1}+\mathrm{G}_{1} \mathrm{G}_{2} \mathrm{G}_{3} \mathrm{H}_{2}}$
(d) $\frac{\mathrm{G}_{1} \mathrm{G}_{2} \mathrm{G}_{3}}{1+\mathrm{G}_{1} \mathrm{G}_{2} \mathrm{G}_{3} \mathrm{H}_{1}}$

R(S) G G H G C(s)

Step by Step Solution

★★★★★

3.27 Rating (165 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

The block diagram shown represents a control system with feedback loops To find the transfer function Cs Rs we need to apply the block diagram reducti... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Systems Analysis And Design Questions!

The diagram shows a right-angled triangle ACD on another right-angled triangle ABC with AD = 26/3 and BC = 2. Show that DC = k2, where k is a constant to be determined. 26 3 3 C 2 B

Obtain a Thvenin equivalent for the circuit of Fig. 4-26 to the left of terminals ab. 10 2 10 2 h 10 2 Is.c. 5 b

The crankshaft AB is rotating at constant angular velocity . Determine the velocity of the piston P for the given . Given: = 150 8 = rad S 30 deg a = 0.2 ft b = 0.75 ft B

Help me solve question 5 and 6 3) The objective of this problem is to learn about building custom counters. Design a block diagram of a counter that counts from 0 to 5 and then resets to 0. When it...

System analysis using Matlab A vehicle suspension system can be modelled by the block diagram shown in Figure 1 below: Body mass m2 Spring of stiffness ks Damper of coefficient cs X Wheel mass, m1...

Problem 2 . Block Diagram Reduction. ( 3 0 points ) Consider a cascade control system that has a block diagram shown below. Figure 2 . 1 Block diagram of a cascade control system In the inner loop, a...

ONLY USING VIVADO PROGRAMMING LANGUAGE . ALSO PLEASE INCLUDE TEST BENCH 2. In the block diagram shown below, the ALU can perform the following 16 operations: REGISTER 1 REGISTER REGISTER AND NAND OR...

ONLY USING VERILOG (VHDL) ONLY USE VERILOG STYLE PROGRAMMING AND PLEASE INCLUDE TEST BENCH In the block diagram shown below, the ALU can perform the following 16 operations: REGISTER 1 ALU REGISTER 3...

of the closed-loop system (c) use the phase margin to determine the maximum magni shown below, convert the block 5. (20 points) For the system represented by the block diagram shown R(s)C(s). diagram...

Problem 4 . Block Diagram and Responses of a Feedforward and Feedforward - Feedback System. ( 2 5 points ) Consider the block diagram shown in the text by Fig. 1 5 . 1 1 . This is repeated below in...

Rock, Paper, Scissors, Lizard, Spock The guys from The Big Bang Theory took the Rock- Paper-Scissors game to a new level: Rules: The game is an expansion on the game Rock, Paper, Scissors. Each...

g Eon Industries is deciding whether to automate one phase of its production process. The manufacturing equipment has a six-year life and will cost $925,000. Projected net cash inflows are as...

make the following piecewise defined function both continuous and dif f ( x ) = { 5 x - 4 , x 1 - x 2 + a x + b , x 1

Training for overseas managers typically focuses on cultural differences, on how attitudes influence behav- ior, and on factual knowledge about the target country. The most common approach to...

There is no acknowledgment mechanism in CSMA/CD, but we need this mechanism in CSMA/CA. Explain the reason.

What is the purpose of NAV in CSMA/CA?

Alice and Bob are experimenting with CSMA using a W 2 Walsh table (see Figure 12.29). Alice uses the code [+1, +1] and Bob uses the code [+1, 1]. Assume that they simultaneously send a hexadecimal...

A dividend is a form of cash flow for a? a. Secured Loan b. Bond c. Debenture d. Share of Common Stock

8. b. What is the LIBOR? What are the lowest/highest levels of the LIBOR since 1990

i need to program a game in c language, using gcc ubuntu compiler. The game that is needed to program is Hangman, please include comments in your code so it can be understood. Is there any libraries...