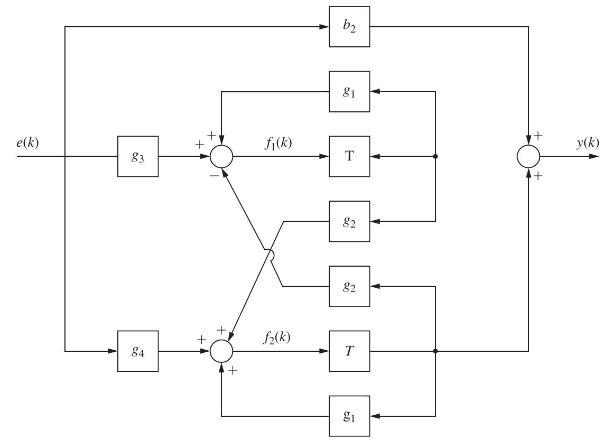
Question: Shown in Fig. P2.8-2 is the second-order digital-filter structure 1X. This structure realizes the filter transfer function [D(z)=b_{2}+frac{A}{z-p}+frac{A^{*}}{z-p^{*}}] where (p) and (p^{*}) (conjugate of (p)
Shown in Fig. P2.8-2 is the second-order digital-filter structure 1X. This structure realizes the filter transfer function
\[D(z)=b_{2}+\frac{A}{z-p}+\frac{A^{*}}{z-p^{*}}\]
where \(p\) and \(p^{*}\) (conjugate of \(p\) ) are complex. The relationships between the filter coefficients and the coefficients in Fig. P2.8-2 are given by
\[\begin{array}{ll} g_{1}=\operatorname{Re}(p) & g_{3}=-2 \operatorname{Im}(A) \\ g_{2}=\operatorname{Im}(p) & g_{4}=2 \operatorname{Re}(A) \end{array}\]
(a) To realize this filter, difference equations are required for \(f_{1}(k), f_{2}(k)\), and \(y(k)\). Write these equations.
(b) Find the filter transfer function \(Y(z) / E(z)\) by taking the \(z\)-transform of the equations of part (a) and eliminating \(F_{1}(z)\) and \(F_{2}(z)\).
(c) Verify the results in part (b) using Mason's gain formula.
(d) Write a computer-program segment that realizes the \(1 \mathrm{X}\) structure. This program should be of the form of that is used in Example 2.10.
Fig. P2.8-2
e(k) 83 f(k) b 81 y(k) T 82 82 + + f(k) 84 T + gi
Step by Step Solution
3.45 Rating (152 Votes )
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


