Three contrasts yield the same Hausman test.

(a) Verify that \(m_{2}\) is numerically exactly identical to \(m_{1}\) and \(m_{3}\), where \(m_{i}=\widehat{q}_{i}^{\prime} V_{i}^{-1} \widehat{q}_{i}\) defined below (4.48).

(b) Verify that these are also exactly numerically identical to \(m_{4}=\widehat{q}_{4}^{\prime} V_{4}^{-1} \widehat{q}_{4}\) where \(\widehat{q}_{4}=\widehat{\beta}_{G L S}-\widehat{\beta}_{O L S}\) and \(V_{4}=\operatorname{var}\left(\widehat{q}_{4}ight)\).

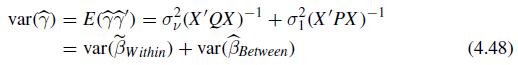
var( EG77) = (X'QX) +o}(X'PX) = var (3within) + var (BBetween) = (4.48)