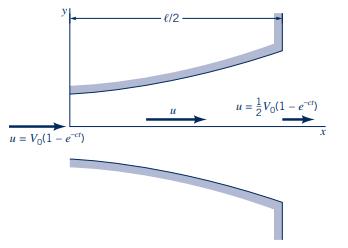
As a valve is opened, water flows through the diffuser shown in Fig. P4.33 at an increasing flowrate so that the velocity along the centerline is given by \(\mathbf{V}=\hat{u} \hat{\mathbf{i}}=V_{0}\left(1-e^{-c t}\right)(1-x / \ell) \hat{\mathbf{i}}\), where \(u_{0}, c\), and \(\ell\) are constants. Determine the acceleration as a function of \(x\) and \(t\). If \(V_{0}=10 \mathrm{ft} / \mathrm{s}\) and \(\ell=5 \mathrm{ft}\), what value of \(c\) (other than \(c=0\) ) is needed to make the acceleration zero for any \(x\) at \(t=1 \mathrm{~s}\) ? Explain how the acceleration can be zero if the flowrate is increasing with time.

Figure P4.33

(-1)=n 212