Water flows over a flat surface at \(4 \mathrm{ft} / \mathrm{s}\), as shown in Fig. P6.42. A pump draws off water through a narrow slit at a volume rate of \(0.1 \mathrm{ft}^{3} / \mathrm{s}\) per foot length of the slit. Assume that the fluid is incompressible and inviscid and can be represented by the combination of a uniform flow and a sink. Locate the stagnation point on the wall (point \(A\) ) and determine the equation for the stagnation streamline. How far above the surface, \(H\), must the fluid be so that it does not get sucked into the slit?

Figure P6.42

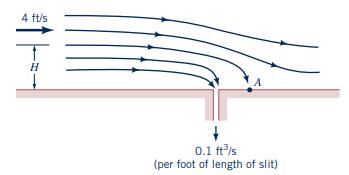
4 ft/s H 0.1 ft/s (per foot of length of slit)