An immediate consequence of Eq. (13.26), is that (modulo a discount factor) it gives, for free, the BSM price of a digital (or binary) option, i.e., an option paying \(\$ 1\) if 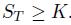. Using the indicator function

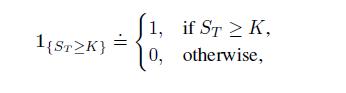
we find

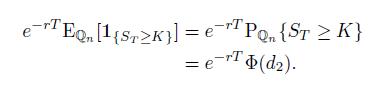
It is important to realize that, in this case, we must calculate \(d_{2}\) using the risk-neutral drift \(r\), as we are pricing the option.
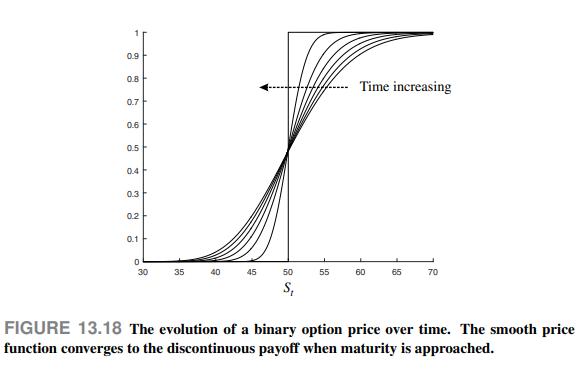
Also note that the binary call features a discontinuous payoff at maturity, but thanks to the parabolic nature of the BSM equation, we find a continuous price as a function of \(S_{t}\). As one may expect, when approaching maturity, the derivative of the option price with respect to \(S_{t}\) will get steeper and steeper, as shown in Fig. 13.18. As we discuss in Section 13.8.3, this could make hedging difficult.

Data From Equation (13.26)

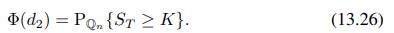
Data From Fig. 13.18

Transcribed Image Text:

STK.