Consider the following proposal. We are offered a lottery, whose outcome is determined by flipping a fair and memoryless coin. The coin is flipped until it lands tails. Let \(k\) be the number of times the coin lands heads; then, the payoff we get is \(\$ 2^{k}\). Now, how much should we be willing to pay for this lottery? Even if we are unlucky and the game stops at the first flip, so that \(k=0\), we will get \(\$ 1\), so we should be willing to pay at least this amount.

We may consider this as an asset pricing problem and set the expected value of the payoff as the fair price for this rather peculiar asset. The probability of winning \(\$ 2^{k}\) is the probability of observing \(k\) consecutive heads followed by the tails that stops the game, after \(k+1\) flips of the coin. Given the independence of events, the probability of this sequence is \(1/2^{k+1}\), i.e., the product of \(k+1\) individual event probabilities. Then, the expected value of the payoff is

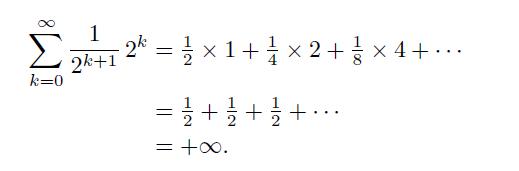
This game looks so beautiful that we should be willing to pay any amount of money to play it! No one would probably do so. True, the game offers huge payoffs, but with vanishing probabilities. Again, we conclude that expected values do not tell the whole story.

Transcribed Image Text:

k=0 1 2k+1 2k = + + 6 / + 1 = +++ = +.