(a) Verify that y = -1 / (x + c) is a one-parameter family of solutions of the differential equation y' = y².

(b) Since f (x, y) = y² and Ï‘f/Ï‘y = 2y are continuous everywhere, the region R in Theorem 1.2.1 can be taken to be the entire xy-plane. Find a solution from the family in part (a) that satisfies y(0) = 1. Then find a solution from the family in part (a) that satisfies y(0) = -1. Determine the largest interval I of definition for the solution of each initial-value problem.

(c) Determine the largest interval I of definition for the solution of the first-order initial-value problem y' = y², y(0) = 0.

Theorem 1.2.1

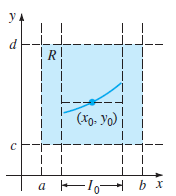
Let R be a rectangular region in the xy-plane defined by a ‰¤ x ‰¤ b, c ‰¤ y ‰¤ d that contains the point (x₀, y₀) in its interior. If f (x, y) and Ï‘f /Ï‘y are continuous on R, then there exists some interval I₀: (x₀ h, x₀ + h), h > 0, contained in [a, b], and a unique function y(x), defined on I0, that is a solution of the initial value problem (2).

 

4 (- l