Given the eigenvalues and eigenvectors for the two degree of freedom system shown in Fig. P5.9, complete the following.
\[\begin{array}{ll}
s_{1}^{2}=-1 \times 10^{6} \mathrm{rad} / \mathrm{s}^{2} & s_{2}^{2}=-7 \times 10^{6} \mathrm{rad} / \mathrm{s}^{2} \\
\Psi_{1}=\left\{\begin{array}{c}
0.5 \\
1 \end{array}\right\} & \Psi_{2}=\left\{\begin{array}{c}
-2.5 \\
1 \end{array}\right\}
\end{array}\]

(a) Determine the modal matrices \(m_{q}(\mathrm{~kg}), c_{q}(\mathrm{~N}-\mathrm{s} / \mathrm{m})\), and \(k_{q}(\mathrm{~N} / \mathrm{m})\).
(b) Plot the imaginary part (in \(\mathrm{m} / \mathrm{N}\) ) of the cross frequency response function, \(X_{1} / F_{2}\). Use a frequency range of \(0: 0.1: 3500 ;(\mathrm{rad} / \mathrm{s})\).

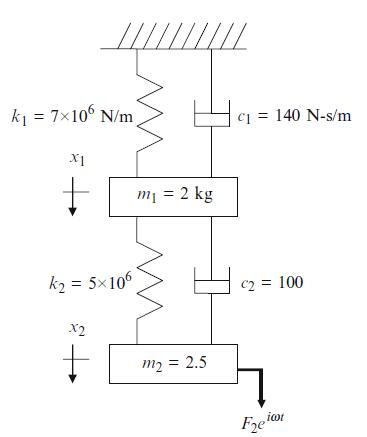
Fig. P5.9 Two degree of freedom spring-massdamper system under forced vibration

////// = k = 7106 N/m c1140 N-s/m X1 m = 2 kg k = 5106 c2 = 100 x2 m2 = 2.5 icot F2e"