Given the eigenvalues and eigenvectors for the two degree of freedom system shown in Fig. P4.1, determine the modal matrices \(m_{q}(\mathrm{~kg}), c_{q}(\mathrm{~N}-\mathrm{s} / \mathrm{m})\), and \(k_{q}(\mathrm{~N} / \mathrm{m})\).
\[\begin{gathered}
s_{1}^{2}=-1 \times 10^{6} \mathrm{rad} / \mathrm{s}^{2} \\
s_{2}^{2}=-7 \times 10^{6} \mathrm{rad} / \mathrm{s}^{2} \\
\psi_{1}=\left\{\begin{array}{c}0.5 \\1
\end{array}\right\} \quad \psi_{2}=\left\{\begin{array}{c}
-2.5 \\
1
\end{array}\right\}\end{gathered}\]

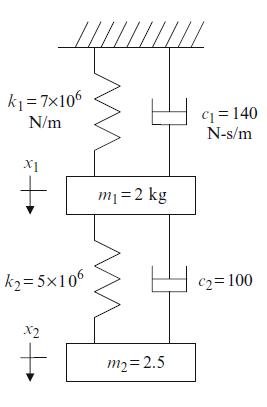
Fig. P4.1 Two degree of freedom spring-mass-damper system

k = 7106 N/m //// x1 m = 2 kg k2=5106 2+ x2 m2=2.5 C=140 N-s/m C2=100