In the structure in Figure P36a, six wires support three beams. Wires 1 and 2 can support no more than 1200 N each, wires 3 and 4 can support no more than 400 N each, and wires 5 and 6 can support no more than 200 N each. Three equal weights W are attached at the points shown. Assuming that the structure is stationary and that the weights of the wires and the beams are very small compared to W, the principles of statics applied to a particular beam state that the sum of vertical forces is zero and that the sum of moments about any point is also zero. Applying these principles to each beam using the free-body diagrams shown in Figure P36b, we obtain the following equations. Let the tension force in wire i be T_i. For beam 1

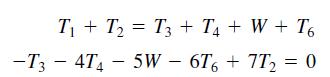
For beam 2

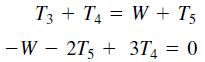
For beam 3

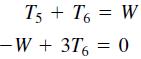
Figure P36

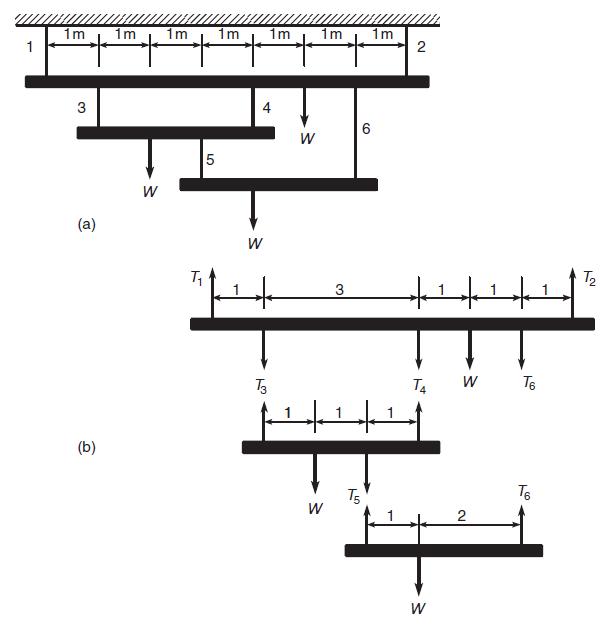
Find the maximum value of the weight W the structure can support. Remember that the wires cannot support compression, so T_i must be nonnegative.

T + T, = T3 + T4 + W+ T6 -T3 - 4T4 - 5W 6T6 + 7T, = 0 |