The force that causes simple harmonic motion in the mass-spring system of Figure P1.41 is \(F(t)=35 \sin 30 t \mathrm{~N}\). The resulting displacement of the mass is \(x(t)=0.002 \sin (30 t-\pi) \mathrm{m}\).

(a) What is the period of the motion?

(b) The amplitude of displacement is \(X=\frac{F_{0}}{k} M\) where \(F_{0}\) is the amplitude of the force and \(M\) is a dimensionless factor called the magnification factor.

Calculate \(M\).

(c) \(M\) has the form

\[ M=\frac{1}{\left|1-\left(\frac{\omega}{\omega_{n}}\right)^{2}\right|} \]

where \(\omega_{n}\) is called the natural frequency. If \(\omega_{n}

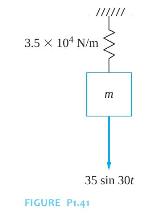
3.5 x 10 N/m m 35 sin 30t FIGURE P1.41