Question: Give a dynamic-programming algorithm for the activity-selection problem, based on recurrence (16.2). Have your algorithm compute the sizes c[I, j] as defined above and also
(16.2)
![if Sij = Ø , max {c[i,k]+ c[k, j]+ 1} _if Sij + Ø . c[i, j]= ak ES¡J](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/1/5/2/5175c192805728f01545135083612.jpg)
(16.1)
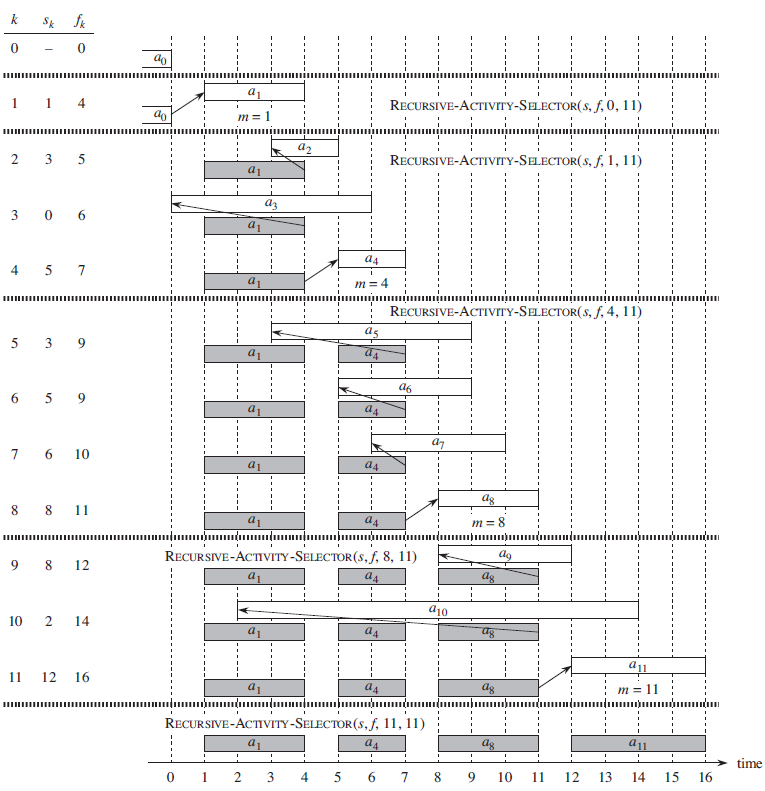
if Sij = , max {c[i,k]+ c[k, j]+ 1} _if Sij + . c[i, j]= ak ESJ a1 RECURSIVE-ACTIVITY-SELECTOR(S, f, 0, 11) 2 3 5 RECURSIVE-ACTIVvrTY-SELECTOR(S, f, 1, 11) a1 3 0 6 a1 a4 4 5 7 m = 4 RECURSIVE-ACTIVITY-SELECTOR(s,f, 4, 11) as 5 a6 6 5 9 7 6 10 a4 ag 8 8 11 a1 nn a4 RECURSIVE-ACTIVITY-SELECTOR(s, f, 8, 11) 12 ag 10 2 14 ug 11 12 16 m = 11: umnum a1 a4 ag RECURSIVE-ACTIVITY-SELECTOR(Ss, f, 11, 11) ag a11 time 3 4 6. 10 11 12 13 14 15 16 9. 3.
Step by Step Solution
3.37 Rating (169 Votes )
There are 3 Steps involved in it
The tricky part is determining which activities are in the set S ij If activitykis inS ij then we mu... View full answer

Get step-by-step solutions from verified subject matter experts


