A pair of random variables has the circular normal distribution if their joint density is given by [begin{aligned}& fleft(x_{1}, x_{2} ight) & quad=frac{1}{2 pi sigma^{2}}

A pair of random variables has the circular normal distribution if their joint density is given by

\[\begin{aligned}& f\left(x_{1}, x_{2}\right) \\& \quad=\frac{1}{2 \pi \sigma^{2}} e^{-\left[\left(x_{1}-\mu_{1}\right)^{2}+\left(x_{2}-\mu_{2}\right)^{2}\right] / 2 \sigma^{2}} \\& \text { for }-\infty

(a) If \(\mu_{1}=2\) and \(\mu_{2}=-2\), and \(\sigma=10\), use Table 3 to find the probability that \(-8

(b) If \(\mu_{1}=\mu_{2}=0\) and \(\sigma=3\), find the probability that \(\left(X_{1}, X_{2}\right)\) is contained in the region between the two circles \(x_{1}^{2}+x_{2}^{2}=9\) and \(x_{1}^{2}+x_{2}^{2}=36\).

Data From Table 3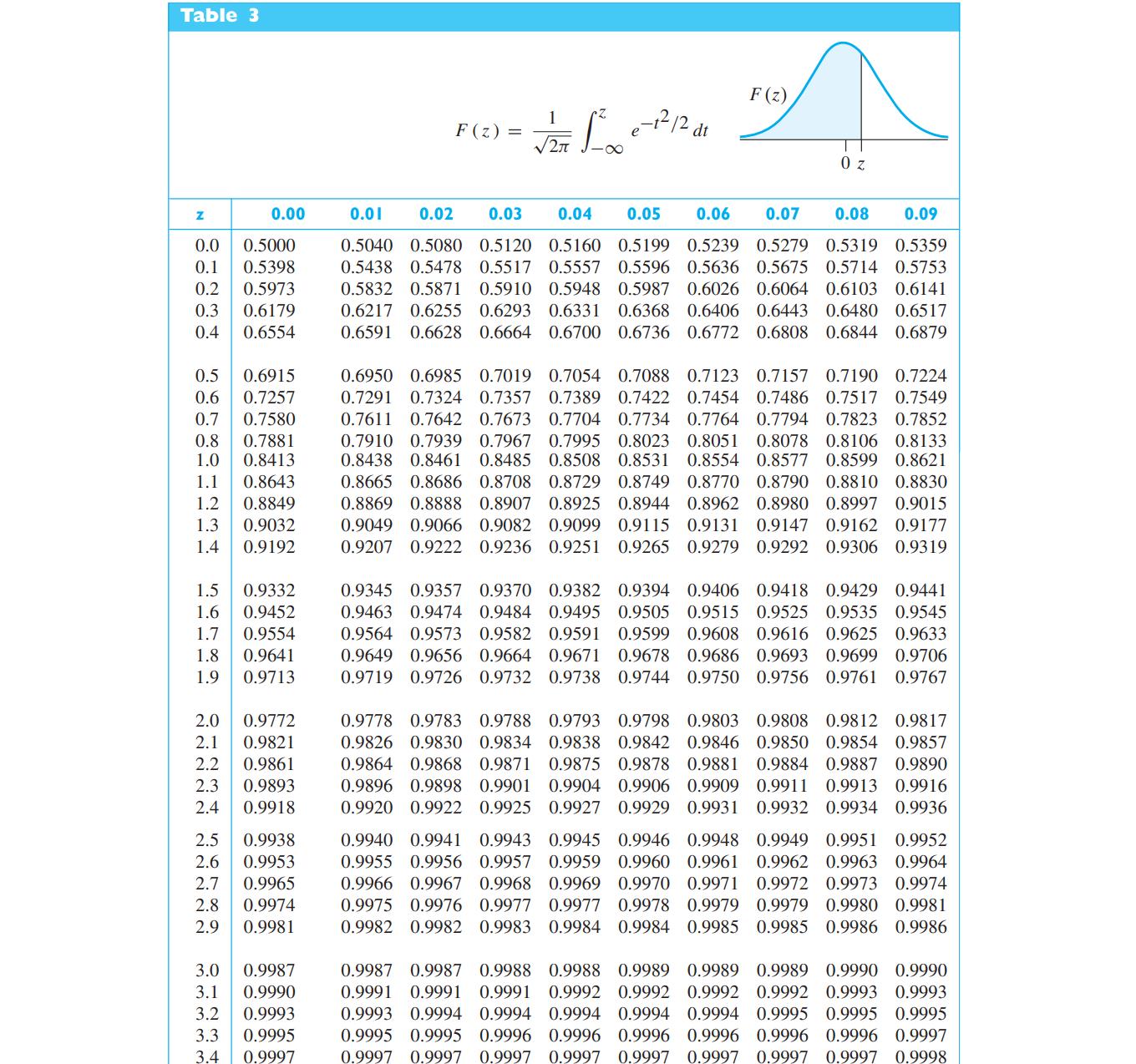

Table 3 Z F(z) = 1 2 -12 12 dt F(z) 0 z 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.0 0.5000 0.1 0.5398 0.2 0.5973 0.3 0.6179 0.4 0.6554 0.5 0.6915 0.6 0.7257 0.7 0.7580 0.8 0.7881 1.0 0.8413 1.1 0.8643 0.8849 0.9032 0.9192 1.2 1.3 1.4 1.5 0.9332 1.6 0.9452 1.7 0.9554 1.8 0.9641 1.9 0.9713 2.0 0.9772 2.1 0.9821 2.2 0.9861 123 2.3 0.9893 2.4 0.9918 2.5 0.9938 2.6 0.9953 2.7 0.9965 619 2.8 0.9974 2.9 0.9981 3.0 0.9987 0.9990 71 3.1 3.2 0.9993 3.3 0.9995 3.4 0.9997 0.5040 0.5080 0.5120 0.5160 0.5199 0.5239 0.5279 0.5319 0.5359 0.5438 0.5478 0.5517 0.5557 0.5596 0.5636 0.5675 0.5714 0.5753 0.5832 0.5871 0.5910 0.5948 0.5987 0.6026 0.6064 0.6103 0.6141 0.6217 0.6255 0.6293 0.6331 0.6368 0.6406 0.6443 0.6480 0.6517 0.6591 0.6628 0.6664 0.6700 0.6736 0.6772 0.6808 0.6844 0.6879 0.6950 0.6985 0.7019 0.7054 0.7088 0.7123 0.7157 0.7190 0.7224 0.7291 0.7324 0.7357 0.7389 0.7422 0.7454 0.7486 0.7517 0.7549 0.7611 0.7642 0.7673 0.7704 0.7734 0.7764 0.7794 0.7823 0.7852 0.7910 0.7939 0.7967 0.7995 0.8023 0.8051 0.8078 0.8106 0.8133 0.8438 0.8461 0.8485 0.8508 0.8531 0.8554 0.8577 0.8599 0.8621 0.8665 0.8686 0.8708 0.8729 0.8749 0.8770 0.8790 0.8810 0.8830 0.8869 0.8888 0.8907 0.8925 0.8944 0.8962 0.8980 0.8997 0.9015 0.9049 0.9066 0.9082 0.9099 0.9115 0.9131 0.9147 0.9162 0.9177 0.9207 0.9222 0.9236 0.9251 0.9265 0.9279 0.9292 0.9306 0.9319 0.9345 0.9357 0.9370 0.9382 0.9394 0.9406 0.9418 0.9429 0.9441 0.9463 0.9474 0.9484 0.9495 0.9505 0.9515 0.9525 0.9535 0.9545 0.9564 0.9573 0.9582 0.9591 0.9599 0.9608 0.9616 0.9625 0.9633 0.9649 0.9656 0.9664 0.9671 0.9678 0.9686 0.9693 0.9699 0.9706 0.9719 0.9726 0.9732 0.9738 0.9744 0.9750 0.9756 0.9761 0.9767 0.9778 0.9783 0.9788 0.9793 0.9798 0.9803 0.9808 0.9812 0.9817 0.9826 0.9830 0.9834 0.9838 0.9842 0.9846 0.9850 0.9854 0.9857 0.9864 0.9868 0.9871 0.9875 0.9878 0.9881 0.9884 0.9887 0.9890 0.9896 0.9898 0.9901 0.9904 0.9906 0.9909 0.9911 0.9913 0.9916 0.9920 0.9922 0.9925 0.9927 0.9929 0.9931 0.9932 0.9934 0.9936 0.9940 0.9941 0.9943 0.9945 0.9946 0.9948 0.9949 0.9951 0.9952 0.9955 0.9956 0.9957 0.9959 0.9960 0.9961 0.9962 0.9963 0.9964 0.9966 0.9967 0.9968 0.9969 0.9970 0.9971 0.9972 0.9973 0.9974 0.9975 0.9976 0.9977 0.9977 0.9978 0.9979 0.9979 0.9980 0.9981 0.9982 0.9982 0.9983 0.9984 0.9984 0.9985 0.9985 0.9986 0.9986 0.9987 0.9987 0.9988 0.9988 0.9989 0.9989 0.9989 0.9990 0.9990 0.9991 0.9991 0.9991 0.9992 0.9992 0.9992 0.9992 0.9993 0.9993 0.9993 0.9994 0.9994 0.9994 0.9994 0.9994 0.9995 0.9995 0.9995 0.9995 0.9995 0.9996 0.9996 0.9996 0.9996 0.9996 0.9996 0.9997 0.9997 0.9997 0.9997 0.9997 0.9997 0.9997 0.9997 0.9997 0.9998