(a) Compute (x) , (p) , (x 2 ) and (p 2 ) , for the states 0 (Equation 2.60) and 1 (Equation

(a) Compute (x) , (p) , (x²) and (p²) , for the states Ψ₀ (Equation 2.60) and Ψ₁ (Equation 2.63), by explicit integration. Comment: In this and other problems involving the harmonic oscillator it simplifies matters if you introduce the variable

and the constant
(b) Check the uncertainty principle for these states.
(c) Compute (T) and (V) for these states. (No new integration allowed!) Is their sum what you would expect?

Equation 2.60

Equation 2.63

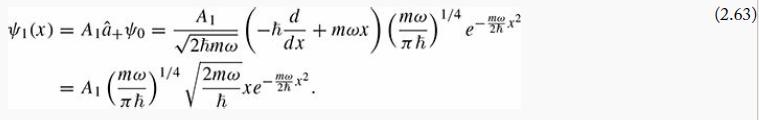
= mo/hx