A free particle has the initial wave function where A and a are (real and positive) constants. (a) Normalize (x,0). (b) Find (x,t).

A free particle has the initial wave function

where A and a are (real and positive) constants.
(a) Normalize Ψ (x,0).
(b) Find Ψ (x,t). Integrals of the form

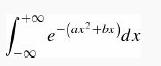
can be handled by “completing the square”: Let

and note that

(ax² + bx) = y² - (b²/4a).

(c) Find |Ψ (x,t)|². Express your answer in terms of the quantity

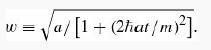
Sketch |Ψ|² (as a function of x) at _t = 0, and again for some very large t. Qualitatively, what happens to |Ψ|², as time goes on?
(d) Find (x), (p) , (x²), (p²), σ_x and σ_p . Partial (p²) = αћ² , but it may take some algebra to reduce it to this simple form.
(e) Does the uncertainty principle hold? At what time t does the system come closest to the uncertainty limit?

(x,0) = Ae-a