Consider a particle constrained to move in two dimensions in the cross-shaped region shown in Figure 8.10. The “arms” of the cross continue out to infinity. The potential is zero within the cross, and infinite in the shaded areas outside. Surprisingly, this configuration admits a positive-energy bound state.

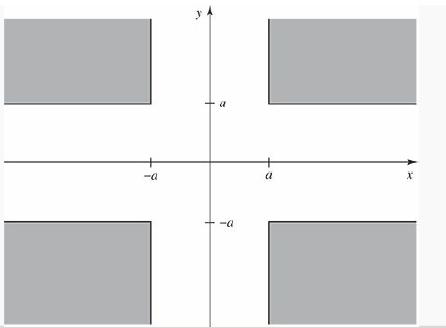
Figure 8.10: The cross-shaped region for Problem 8.27.

(a) Show that the lowest energy that can propagate off to infinity is

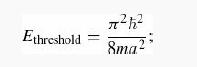
any solution with energy less than that has to be a bound state.
(b) Now use the variational principle to show that the ground state has energy less than E_threshold. Use the following trial wave function (suggested by Jim McTavish):

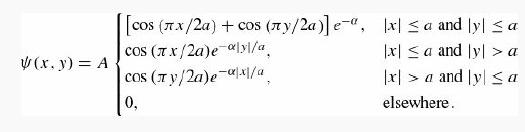
Normalize it to determine A, and calculate the expectation value of H.

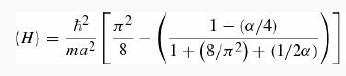
Now minimize with respect to α, and show that the result is less than E_threshold.

X D) -a