In Problem 8.8 we found that the trial wave function with shielding (Equation 8.28), which worked well for helium, is inadequate to confirm the existence of a bound state for the negative hydrogen ion. Chandrasekhar used a trial wave function of the form

where

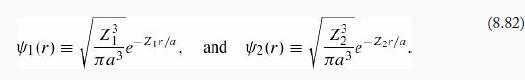
In effect, he allowed two different shielding factors, suggesting that one electron is relatively close to the nucleus, and the other is farther out. (Because electrons are identical particles, the spatial wave function must be symmetrized with respect to interchange. The spin state—which is irrelevant to the calculation—is evidently antisymmetric.) Show that by astute choice of the adjustable parameters Z₁ and Z₂ you can get (H) less than -13.6 eV.

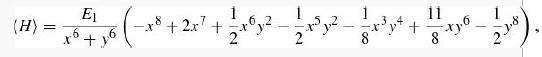
where x Ξ Z₁ + Z₂ and y  Ξ 2√Z₁Z₂. Chandrasekhar used Z₁ = 1.039 (since this is larger than 1, the motivating interpretation as an effective nuclear charge cannot be sustained, but never mind—it’s still an acceptable trial wave function) and Z₂ = 0.283.

(r, r2) = A[V1 (1)2(12) + 2(1)(2)], (8.81)