Let (left{X_{n}ight}_{n=1}^{infty}) be a sequence of independent and identically distributed random variables from a density of the
Question:
Let \(\left\{X_{n}ight\}_{n=1}^{\infty}\) be a sequence of independent and identically distributed random variables from a density of the form \[f(x)= \begin{cases}c x^{2} \log (|x|) & |x|>2 \\ 0 & |x| \leq 2\end{cases}\] where \(c\) is a normalizing constant. Prove that \(n P\left(\left|X_{1}ight|>night) ightarrow 0\) as \(n ightarrow \infty\), but that the mean does not exist. Hence, we can still conclude that \(\bar{X}_{n} \xrightarrow{p} 0\) as \(n ightarrow \infty\) due to Theorem 3.14.
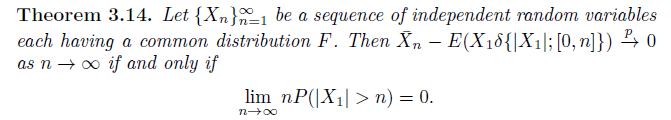
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





