A function (f: mathbb{R}^{n} ightarrow mathbb{R}) is called convex if for any (mathbf{x}, mathbf{y} in mathbb{R}^{n}) and (t in[0,1]) Show that a non-constant convex

A function \(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) is called convex if for any \(\mathbf{x}, \mathbf{y} \in \mathbb{R}^{n}\) and \(t \in[0,1]\)

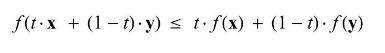
Show that a non-constant convex function defined on a bounded convex set cannot take on its maximum value in the interior of the convex set.

f(tx (1) y) tf(x) + (1-t) f(y) f(x(t)