Consider a probit model explaining the choice to attend a 4-year college rather than a 2 -year college by high-school graduates who chose to attend a postsecondary school. Define \(F O U R Y R=1\) if a high-school graduate chooses 4-year college and FOURYR \(=0\) if the high school graduate chooses a 2-year college. We use explanatory variables GRADES, 13 point scale with 1 indicating highest grade (A+) and 13 the lowest \((\mathrm{F}) ;\) FAMINC, gross family income in \(\$ 1000\) units; and HSCATH \(=1\) if the student attended a Catholic high school and \(H S C A T H=0\) otherwise. Table 16.9 contains some probit model estimates.

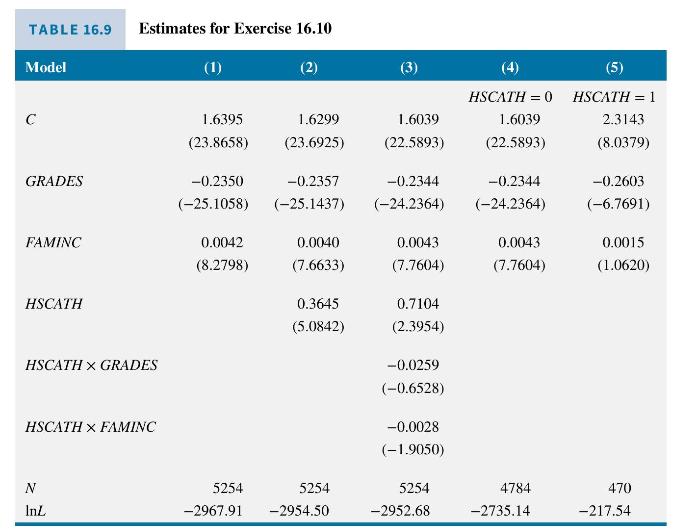
a. Using Model (2), how large an effect on the probability of attending a 4-year college does attending a catholic high school have for a student with \(G R A D E S=5\) (B) and family income of \(\$ 100,000\).

b. Comparing Models (2) and (3), are the interaction variables HSCATH \(\times\) GRADES and \(H S C A T H \times\) FAMINC jointly significant at \(5 \%\) using a likelihood ratio test?

c. Can we interpret the Model (3) results as saying an increase in family income reduces the probability of attending a 4-year college for someone graduating from a Catholic high school? What is the marginal effect of an additional \(\$ 1000\) in family income for a Catholic high school student with GRADES \(=5\) (B) and family income of \(\$ 50,000\) ?

d. Using Model (3), compute the probability of attending a 4-year college for someone graduating from a Catholic high school with GRADES \(=5\) (B) and family income of \(\$ 100,000\). Compare this probability to a student who did not attend a Catholic high school but has GRADES \(=5\) (B) and family income of \(\$ 100,000\).

e. Using Models (1) and (3), test the null hypothesis that the probit model parameters are the same for students who attend and do not attend a Catholic high school. Use a likelihood ratio test at the \(5 \%\) level of significance.

f. Using Models (4) and (5), estimate the probit model separately for \(H S C A T H=0\) and \(H S C A T H=1\). Compute the sum of the log-likelihood functions values. Compare the sum to the log-likelihood for Model (3). Algebraically show that this is not an accident.

TABLE 16.9 Estimates for Exercise 16.10 Model (2) (4) (5) HSCATH = 0 HSCATH=1 C 1.6395 1.6299 1.6039 1.6039 2.3143 (23.8658) (23.6925) (22.5893) (22.5893) (8.0379) GRADES -0.2350 -0.2357 (-25.1058) (-25.1437) -0.2344 (-24.2364) -0.2344 (-24.2364) -0.2603 (-6.7691) FAMINC 0.0042 0.0040 0.0043 0.0043 0.0015 (8.2798) (7.6633) (7.7604) (7.7604) (1.0620) HSCATH 0.3645 0.7104 (5.0842) (2.3954) HSCATH X GRADES -0.0259 HSCATH FAMINC N InL (-0.6528) -0.0028 (-1.9050) 5254 -2967.91 5254 -2954.50 5254 -2952.68 4784 -2735.14 470 -217.54