Consider the data file \(m r o z\) on working wives. Use the 428 observations on married women who participate in the labor force. In this exercise, we examine the effectiveness of a parent's college education as an instrumental variable.

a. Create two new variables. MOTHERCOLL is a dummy variable equaling one if MOTHEREDUC > 12, zero otherwise. Similarly FATHERCOLL equals one if FATHEREDUC > 12, and zero otherwise. Also, create COLLSUM \(=\) MOTHERCOLL + FATHERCOLL and COLLBOTH \(=\) MOTHERCOLL \(\times\) FATHERCOLL. What values do COLLSUM and COLLBOTH take? What percentage of women in the sample have both a mother and a father with some college education.

b. Find the correlations between EDUC, COLLSUM, and COLLBOTH. Are the magnitudes of these correlations important? Can you make a logical argument why COLLSUM and COLLBOTH might be better instruments than MOTHEREDUC and FATHEREDUC?

c. Estimate the wage equation in Example 10.5 using 2SLS with COLLSUM as the instrumental variable. What is the \(95 \%\) interval estimate for the coefficient of \(E D U C\) ?

d. For the problem in part (c), estimate the first-stage equation. What is the value of the \(F\)-test statistic for the hypothesis that COLLSUM has no effect on EDUC? Is COLLSUM a strong instrument?

e. Using OLS estimate the regression model with \(E D U C\) as dependent variable, and include as explanatory variables experience, and its square, along with MOTHERCOLL and FATHERCOLL, and a constant term. Test the null hypothesis that the coefficients of MOTHERCOLL and FATHERCOLL are equal at the \(5 \%\) level.

f. Based on the results in part (e), are we justified in using COLLSUM \(=\) MOTHERCOLL + FATHERCOLL as an IV? Are we better off using COLLSUM only or using MOTHERCOLL and FATHERCOLL?

Data From Example 10.5:-

In addition to education a worker's experience is also important in determining their wage. Because additional years of experience have a declining marginal effect on wage use the quadratic model 

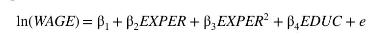
where EXPER is years of experience. This is the same specification. We assume that EXPER is an exogenous variable that is uncorrelated with the worker's ability and therefore uncorrelated with the random error \(e\). Two instrumental variables for years of education, \(E D U C\), are mother's and father's years of education, MOTHEREDUC and FATHEREDUC, introduced in the previous examples. The first-stage equation is  

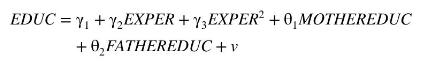
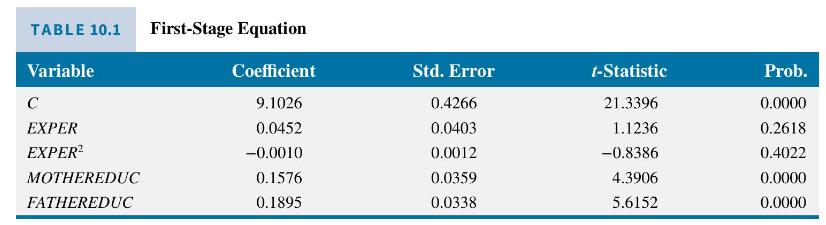
Using the 428 observations in the data file mroz the estimated first-stage equation is reported in Table 10.1. The IV/2SLS estimates, with correctly computed standard errors, are

The estimated return to education is approximately \(6.1 \%\), and the estimated coefficient is statistically significant with a \(t=1.96\).

Transcribed Image Text:

In(WAGE) = B+ BEXPER+ BEXPER + BEDUC + e