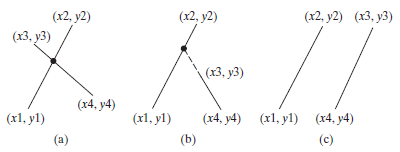
Question: Two points on line 1 are given as (x1, y1) and (x2, y2) and on line 2 as (x3, y3) and (x4, y4), as shown
Two points on line 1 are given as (x1, y1) and (x2, y2) and on line 2 as (x3, y3) and (x4, y4), as shown in Figure 3.8a?b.
 The intersecting point of the two lines can be found by solving the following linear equation:
The intersecting point of the two lines can be found by solving the following linear equation:
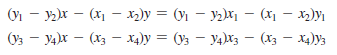
This linear equation can be solved using Cramer?s rule (see Programming Exercise 3.3). If the equation has no solutions, the two lines are parallel (Figure 3.8c).Write a program that prompts the user to enter four points and displays the intersecting point. Here are sample runs:
Enter x1, yl, x2, y2, x3, y3, x4, y4: 2 2 5 -1.0 4.0 2.0 -1.0 -2.0 The intersecting point is at (2.88889, 1.1111) JEnter Enter x1, yl, x2, y2, x3, y3, x4, y4: 2 2 7 6.0 4.0 2.0 -1.0 -2.0 Jerter The two lines are parallel (yi - x (x - x2)y = (y y2x (x x2)y (V3 - Y4)x (x3 x4)y = (V3 Y4)X3 (X3 X4)y3
Step by Step Solution
3.45 Rating (164 Votes )
There are 3 Steps involved in it
Sample output Enter x1 y1 x2 y2 x3 y3 y4 y4 2 2 5 10 40 20 10 20 The intersecting point at288... View full answer

Get step-by-step solutions from verified subject matter experts


