A simple well-known game, tic-tac-toe, is played on a three-by-three grid of squares by two players. The players alternate turns. Each player chooses a square and places a mark in a square. (One player uses X and the other O.)
The irst player with three marks in a row, in a column, or on a diagonal wins the game. A logic circuit is to be designed for an electronic tic-tac-toe that indicates the presence of a winning pattern. The circuit output W is a 1 if a winning pattern is present and a 0 if a winning pattern is not present. For each of the nine squares, there are two signals, X_i and O_i . Two copies of the circuit are used, one for Xs and one for Os. Form a condensed truth table for W(X₁, X₂, . . . . X₉).

(a) Design the X circuit for the following pattern of signals for the squares:

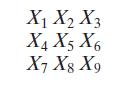
(b) Minimize the W output for the X circuit as much as possible, using Boolean algebra.

Transcribed Image Text:

X X X3 X4 X5 X6 X7 X8 X9