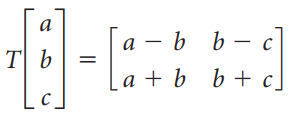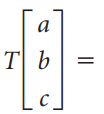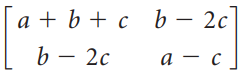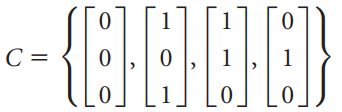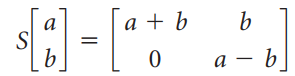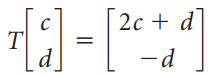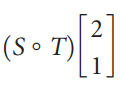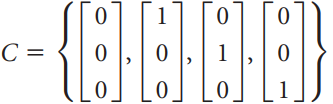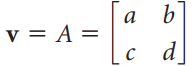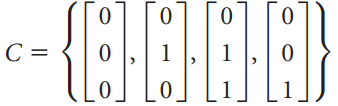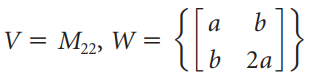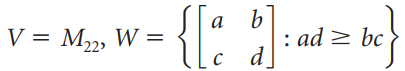![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


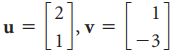
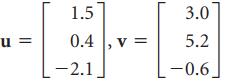
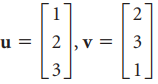
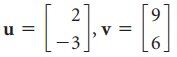
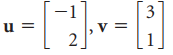
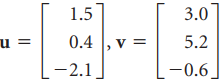
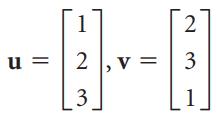
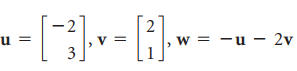
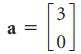
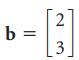
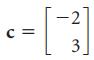
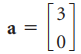
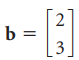
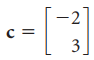
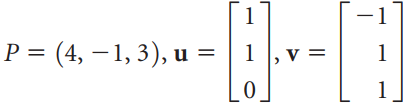
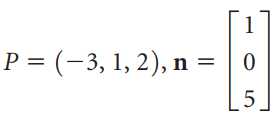
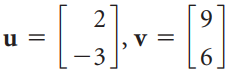
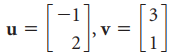
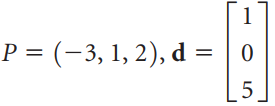
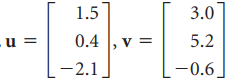
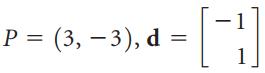
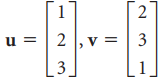
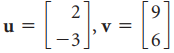
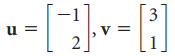
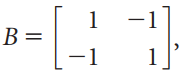
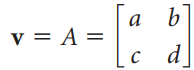
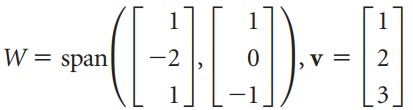
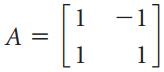
![w + x х y – z] I|](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1536/1/5/9/3155b8fee53d2abe1536141638739.jpg)
![[p(0)° Lp(1)] ||](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1536/2/2/8/3125b90fbd8ebb931536210645393.jpg)
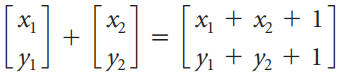
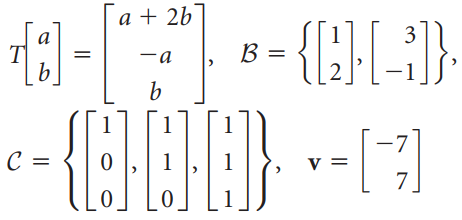
![Find the matrix [T] C←B of the linear transformation T](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1536/2/2/8/8095b90fdc95d8cf1536211141768.jpg)
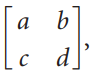
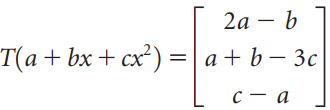
![p(0) ] T(p(x)) Lp(1).](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1536/1/6/7/1665b900cfe435271536149488546.jpg)