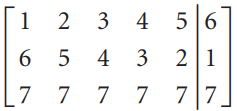
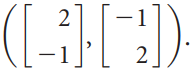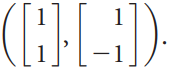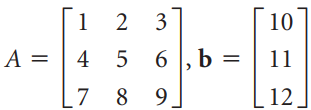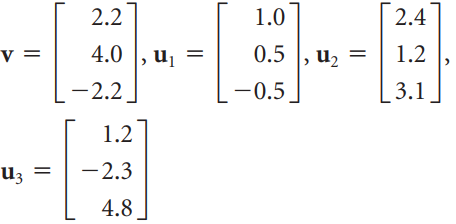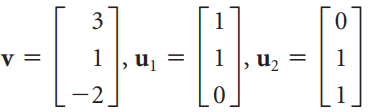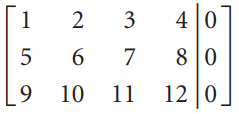![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


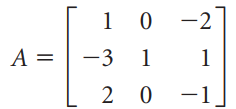
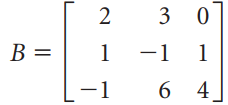
![2 1 C = 3 |A = 4 B = -2 3 4 2 3 5 5 6 -3 E = [4 2], F= D = %3D 2.](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1535/3/6/9/3155b83e0632b0451535351615524.jpg)
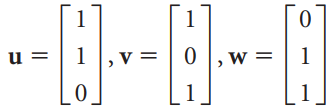
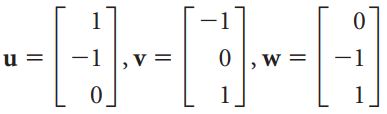
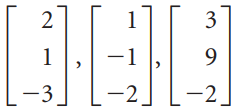
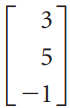
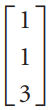
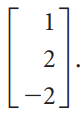
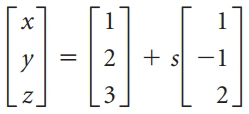
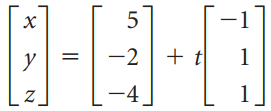
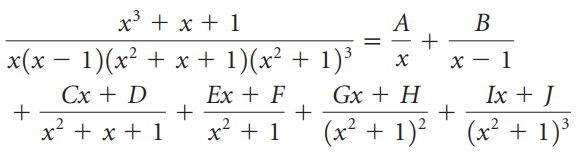
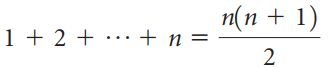
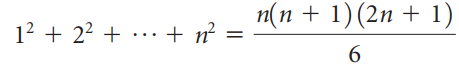
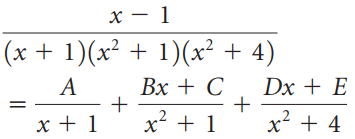
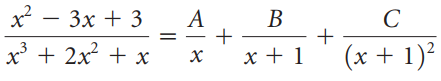
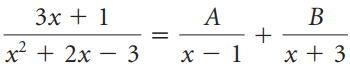
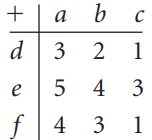
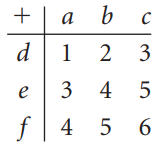
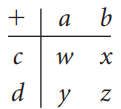
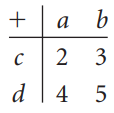
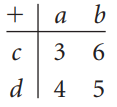
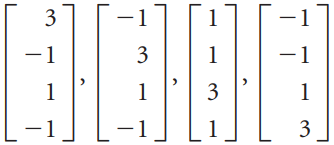
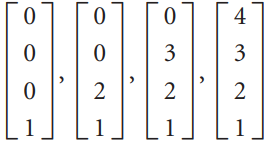
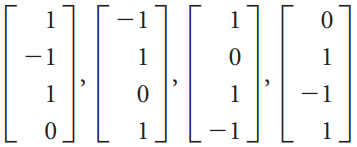
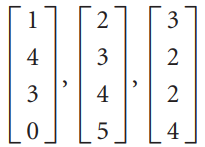
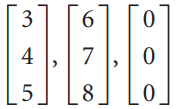
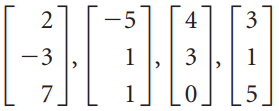
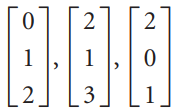
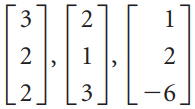
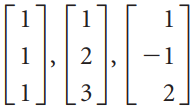
![-2° 3 4 -1]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1535/1/9/5/3385b8138ca026b71535177638612.jpg)
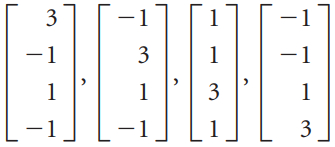
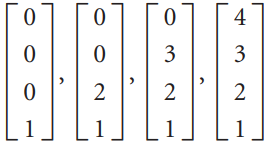
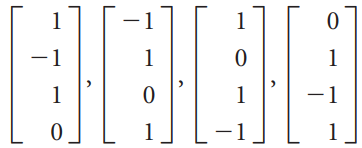
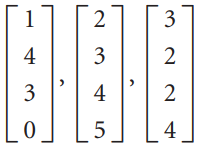
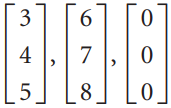
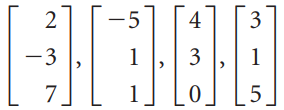
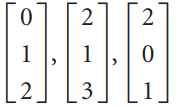
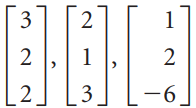
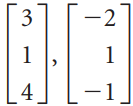
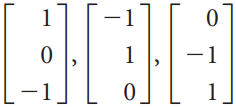
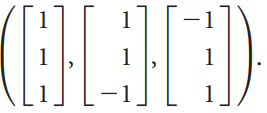
![L0]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1535/1/9/3/0995b81300b565f11535175399177.jpg)