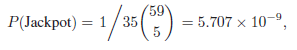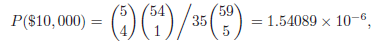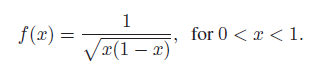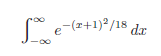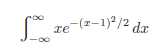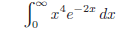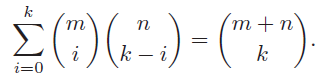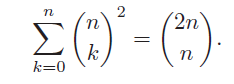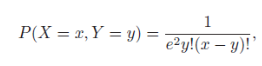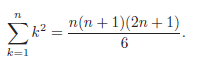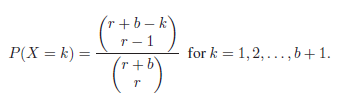![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


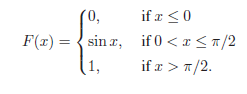
![η (п+1)п) n +1 Π Σα -P(X - ) Σ ΕΙX]- 2 T=1](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1539/2/5/5/6735bbf2d793799c1539238103473.jpg)
![EX]Σ2, style=](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1539/1/8/0/1415bbe066d8629d1539162567389.jpg)