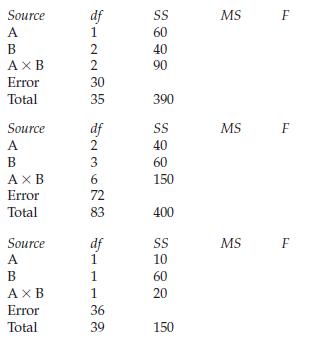
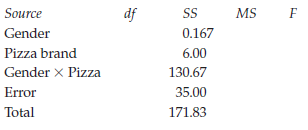
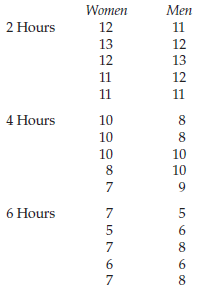
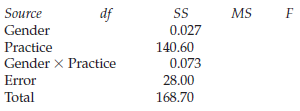
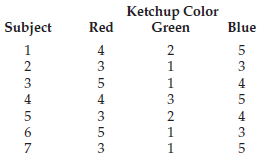
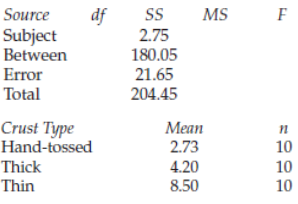
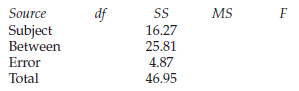
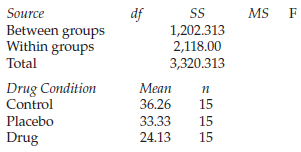
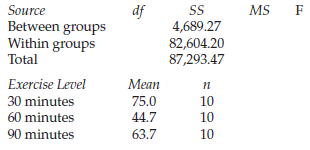
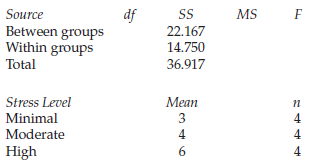
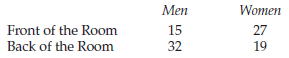Research Methods And Statistics A Critical Thinking Approach 5th Edition Sherri L. Jackson - Solutions

Discover comprehensive resources for "Research Methods And Statistics: A Critical Thinking Approach 5th Edition" by Sherri L. Jackson. Access the online answers key, providing solutions to textbook questions and answers. Delve into the solution manual and solutions pdf, offering step-by-step answers and solved problems for each chapter. Enhance your study with the test bank and chapter solutions, ensuring a thorough understanding of the material. The instructor manual and textbook insights are available for free download, supporting your educational journey with reliable and accessible content. Unlock the full potential of your learning experience today!