Let \((\Omega, \mathscr{A}, \mathbb{P})\) be a probability space. Adapt the proof of Theorem 22.9 to show that a sequence \(\left(u_{n}ight)_{n \in \mathbb{N}} \subset \mathcal{L}^{1}(\mu)\) is uniformly integrable if it is bounded in some space \(\mathcal{L}^{p}(\mathbb{P})\) with \(p>1\), i.e. if \(\sup _{n \in \mathbb{N}}\left\|u_{n}ight\|_{p}

Use Vitali's convergence theorem to construct an example illustrating that \(\mathcal{L}^{1}\) boundedness of \(\left(u_{n}ight)_{n \in \mathbb{N}}\) does not guarantee uniform integrability.

Data from theorem 22.9

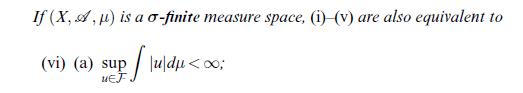
Transcribed Image Text:

Theorem 22.9 Let (X, A, ) be some measure space and FCL(A). Then the following statements (i)-(v) are equivalent: (i) F is uniformly integrable, i.e. (22.1) holds; (ii) (a) supu d 0 WEL (A), 5>0 VBA, (iii) (a) supu Swee We d < 6: sup / \u\ d < ; B uEJ JB d 0 KEA, H(K) 0 VBA, (B) <8: sup 2 | Judul <6; uEJ B (iv) (a) supu d 0KA, (K) 0_\8>0\B(B) <8 : sup | \u\d 0 KEA, (K) R} uEJ J K